La densità critica e il destino dell’universo

Qual è il destino dell’universo? La risposta a questa domanda affascinante risiede nel concetto di densità critica, un parametro chiave che determina la geometria e il futuro cosmico.
Dall’espansione scoperta da Hubble alla curvatura dello spazio-tempo descritta nei modelli di Friedmann.
Comee la densità critica influenza la possibilità di un universo eterno, in contrazione o in equilibrio? Scopri il ruolo dell’energia oscura e come la matematica e la fisica cosmologica lavorino insieme per svelare i misteri del cosmo.
La relatività generale e la geometria dell’universo
 Nel 1915, Albert Einstein pubblicò la teoria della relatività generale, che descrive la gravità come la curvatura dello spazio-tempo causata dalla presenza di massa ed energia. Questo cambiò radicalmente la nostra comprensione dell’universo. La relatività generale portò anche a una visione dinamica dell’universo, che, inizialmente considerato statico, si rivelò invece in espansione.
Nel 1915, Albert Einstein pubblicò la teoria della relatività generale, che descrive la gravità come la curvatura dello spazio-tempo causata dalla presenza di massa ed energia. Questo cambiò radicalmente la nostra comprensione dell’universo. La relatività generale portò anche a una visione dinamica dell’universo, che, inizialmente considerato statico, si rivelò invece in espansione.
Einstein stesso introdusse la costante cosmologica (Λ) per mantenere il modello statico, ma abbandonò questa idea dopo che Edwin Hubble osservò l’espansione dell’universo. Da allora, i modelli cosmologici si sono evoluti, portando alla formulazione della densità critica, che è essenziale per comprendere la geometria e il destino finale dell’universo.
La costante di Hubble
Nel 1929, Edwin Hubble scoprì che le galassie si allontanano l’una dall’altra, rivelando che l’universo è in espansione.
La legge di Hubble stabilisce che la velocità di allontanamento di una galassia è direttamente proporzionale alla sua distanza dalla Terra. In altre parole, la velocità di recessione delle galassie aumenta con la distanza, un concetto fondamentale che si lega alla costante di Hubble, un valore che esprime questa relazione.
La costante di Hubble ha un ruolo cruciale nel determinare la velocità di espansione dell’universo, e la sua conoscenza è essenziale per calcolare la densità critica dell’universo. Questa scoperta implicò che l’universo fosse omogeneo e isotropo, e l’espansione fosse uniforme ovunque. L’espansione dell’universo è legata alla quantità di materia ed energia, e la geometria dell’universo è influenzata dalla densità critica, che determina se l’universo sarà piatto, chiuso o aperto.
La curvatura dell’universo e i modelli di Friedmann
I modelli cosmologici sviluppati da Alexander Friedmann, partendo dalle equazioni della relatività generale, forniscono una visione matematica ed evolutiva dell’universo. Questi modelli evidenziano come la densità di materia ed energia nell’universo determini la sua curvatura spaziale.
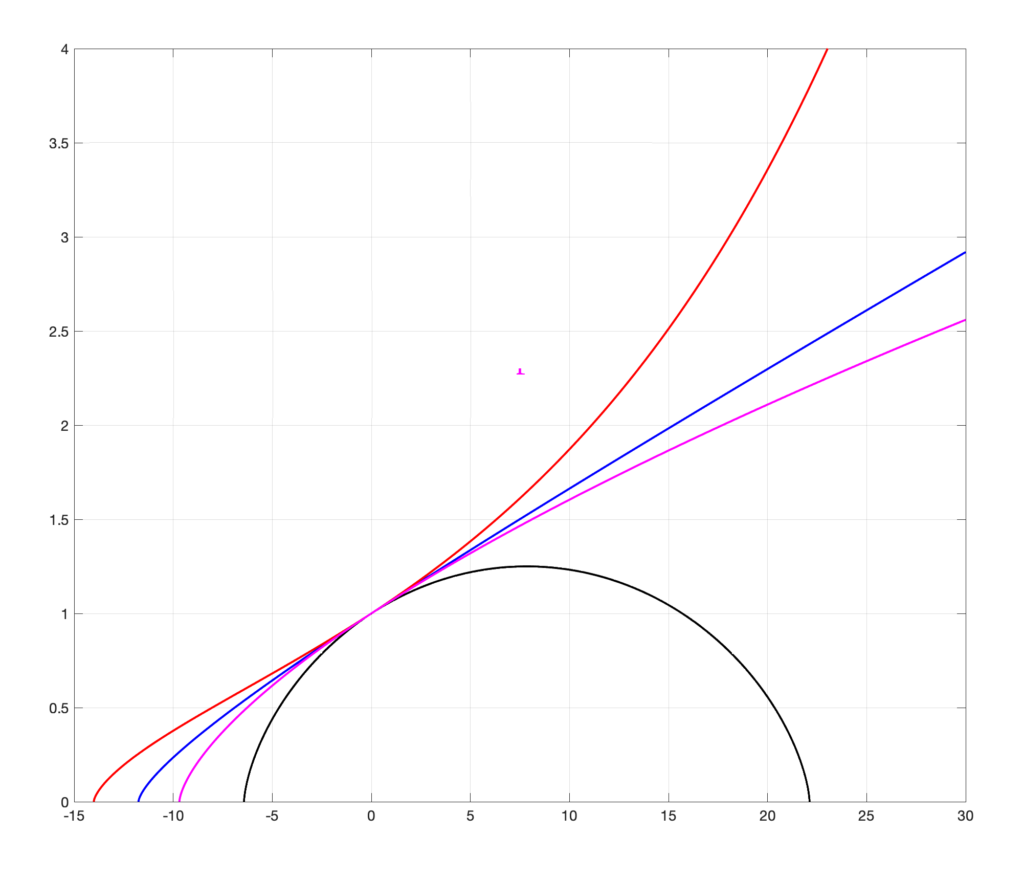
I modelli di Friedmann sono direttamente legati ai concetti di curvatura spaziale (K) che può essere positiva, negativa o nulla e dal rapporto tra densità reale di massa dell’Universo e densità critica indicato con la lettera Ω.
Tabella riassuntiva dei tre modelli di Friedmann
| Densità (Ω) | Curvatura spaziale (K) | Modello geometrico | Destino dell’universo | Espansione futura |
|---|---|---|---|---|
| Ω > 1 | Positiva (K = +1) | Sferica | Big Crunch | Rallenta, si ferma e collassa |
| Ω = 1 | Nulla (K = 0) | Euclidea (piatta) | Espansione infinita | Rallenta senza fermarsi mai |
| Ω < 1 | Negativa (K = -1) | Iperbolica | Big Freeze | Espansione accelerata all’infinito |
Il modello di Universo chiuso (K=+1)
Nel modello di universo chiuso, la densità di materia ed energia supera la densità critica (Ω>1) . Questo comporta una curvatura positiva dell’universo e una geometria sferica.
La conseguenza di questa curvatura è che l’universo non continuerà a espandersi all’infinito, ma la sua espansione rallenterà e infine si invertirà, portando a una contrazione fino a un “Big Crunch” in cui l’intero universo potrebbe collassare su se stesso.
Il modello di universo aperto (K= -1)
Nel modello di universo aperto, la densità è inferiore alla densità critica (Ω<1) , il che provoca una curvatura negativa dello spazio e una geometria iperbolica.
In questo scenario, l’universo si espande indefinitamente senza mai rallentare significativamente. Le galassie continueranno ad allontanarsi le une dalle altre, con una velocità che non si ferma mai, in un’espansione perpetua.
Universo piatto (K=0)
Se la densità dell’universo è esattamente uguale alla densità critica (Ω=1), l’universo ha una curvatura nulla, cioè sarà “piatto”, con una geometria euclidea. In questo caso, l’espansione dell’universo continua per sempre, ma a una velocità che non rallenta mai completamente. La densità è perfettamente bilanciata, l’espansione continua all’infinito.
La densità critica e il futuro dell’universo
La densità critica è il valore teorico della densità di massa ed energia dell’universo che determina la sua geometria e il suo destino a lungo termine. Essa rappresenta la soglia che separa un universo che si espande indefinitamente da uno che eventualmente si contrarrà.
In pratica, la densità effettiva dell’universo, espressa dal parametro Ω, determina il destino cosmico, separando i modelli di espansione eterna, collasso o equilibrio. È calcolata in funzione della costante di Hubble e della gravità.
Scenari di universo statico o in contrazione
Se Ω>1, l’universo è chiuso e si espanderà fino a un punto in cui l’espansione rallenterà, invertendo direzione e iniziando una fase di contrazione, noto come “Big Crunch”. Sebbene teoricamente possibile, questo scenario è meno supportato dalle attuali osservazioni, che suggeriscono una densità inferiore alla densità critica.
L’espansione eterna e l’energia oscura
Con Ω<1, l’universo è aperto e continuerà a espandersi indefinitamente, con una velocità che non rallenta mai significativamente. L’energia oscura, un’ipotetica forma di energia che agisce in senso opposto alla gravità, gioca un ruolo cruciale in questa espansione accelerata. Se l’energia oscura domina, l’universo potrebbe proseguire l’espansione per un tempo infinito.
La densità critica rappresenta una soglia fondamentale per comprendere non solo la geometria dell’universo, ma anche il suo destino finale.
Sebbene molte domande rimangano aperte, il continuo studio della densità critica e dei parametri cosmologici ci avvicina sempre di più alla comprensione dell’universo e del nostro posto in esso.
Credit immagine iniziale: ESO/J. Emerson/VISTA. Acknowledgment: Cambridge Astronomical Survey Unit

